Alternating Group

In this post, I want to try to give a mostly-visual proof of an exercise I found in Dixon's book "Problems in Group Theory":

Show that the alternating group A4 has no subgroup of order 6.

Let's first note that A4 has order 12 and that according to Lagrange's theorem, a subgroup of order 6 could be possible because 6 divides 12.

We can also observe that A4 has a subgroup of order 4. Look at its multiplication table's upper left 4x4 block. The block contains the identity (black) in every row an column and there are only four colors involved.

Let's assume that A4 had a subgroup, call it H, of order 6. Then it had to be isomorphic to the symmetric group of order 3. This is because there are only 2 groups of order 6 and A4 has no elements of order 6 and can therefore not be isomorphic to the cyclic group of order 6.

As a side note, the fact that one can list all groups that exist, up to a certain finite order, was something I found surprising when I read it initially. It's kind of cool that you can make a complete table of the groups of low order.

Next, we check that there are no elements of order 6 in the group and that it therefore cannot be isomorphic to the cyclic group of order 6. A4's cycle diagram below only shows 2-cycles and 3-cycles.

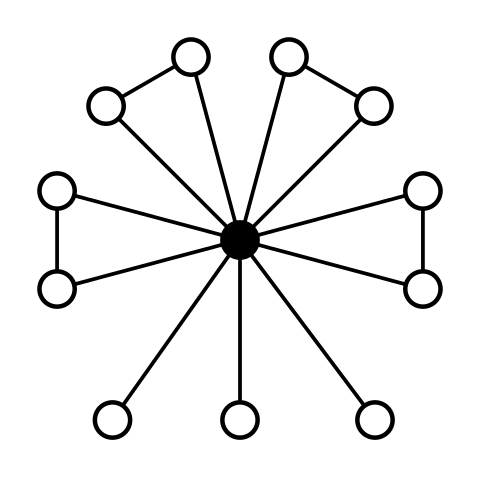
Let's take stock:

1. If our subgroup H < A4 of order 6 existed, it would be isomorphic to S3. But S3 is a group that contains 3 elements of order 2, see below diagram.
2. A4 also has a subgroup of order 4 containing its only 3 elements of order 2.

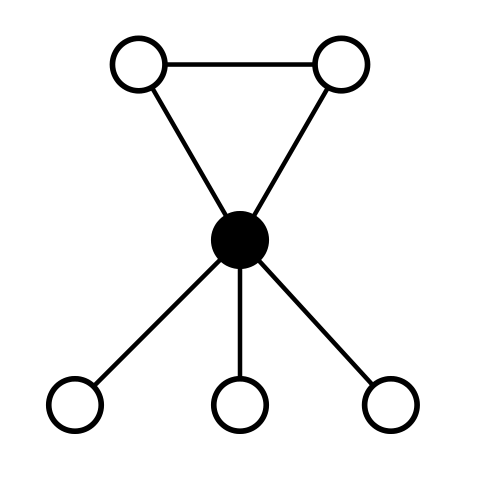
This implies that H would have to contain a subgroup of order 4. But that's a contradiction to Lagrange's theorem which states that every subgroup's order has to divide the group's order. Therefore, H cannot exist and there is no subgroup of order 6 inside A4.

Thanks for reading and thanks to the author of this answer on math stackexchange: https://math.stackexchange.com/a/1334010

Note to self: SVG files with transparent background and black content don't work well on dark background